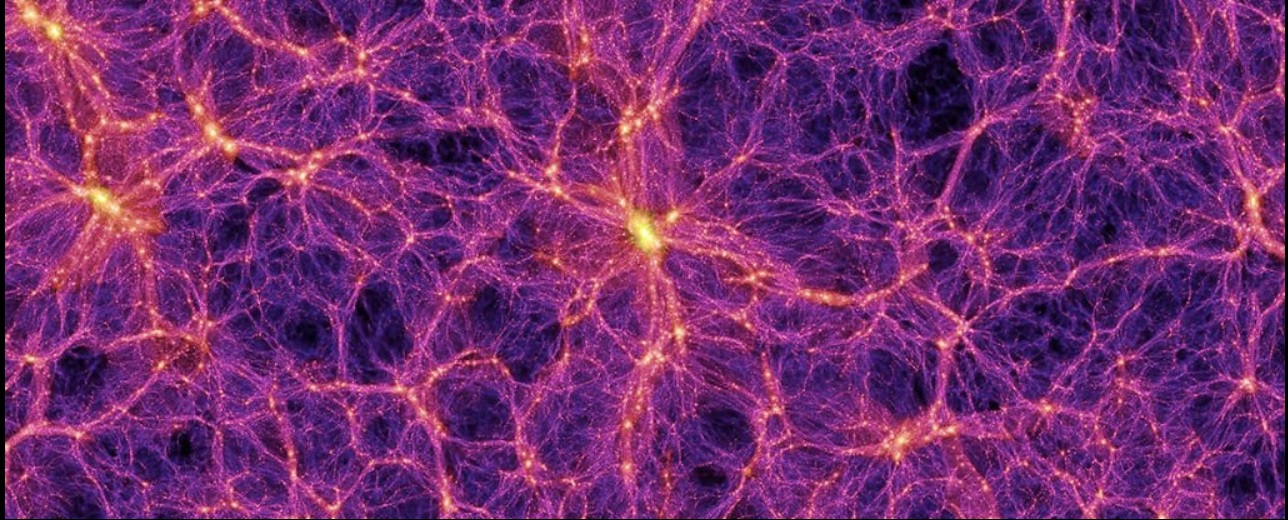
Oggi tutto deve essere uno scoop. Adesso va di moda che ti mostrano l’universo a mo’ di ragnatela, a filamenti. Tutto bene, ma quanto si estende? Cioè quanti filamenti ci sono? Non te lo dicono, perché farebbe meno scoop.
Così ho fatto qualche conto della serva, tanto per capire di che si sta parlando. Mi interessano solo le scale di grandezza, per cui che la Via Lattea sia lunga 100k anni-luce o 250k non mi cambia niente [alla fine cambierò idea].
La nostra “unità di misura concettuale” sarà proprio la Via Lattea (VL), perché siamo in grado di concepirla dimensionalmente (ci sono tanto di foto stupendissime, sul web). VL sta nel Gruppo Locale (GL), che è 100 volte più grande (importante!: misure lineari, perché poi dovremo cubare il tutto). Dal GL passiamo all’ammasso della Vergine e poi al Superammasso Laniakea, che è quello che ci interessa di più, perché qui la descrizione è già solo “a filamenti”. Laniakea è 5 volte la Vergine, e fa 520 milioni di anni-luce. Perciò in Laniakea ci stanno 5.200 Via Lattea, come lunghezza. È un bel numero, ma tutt’altro che ingestibile e inimmaginabile.
Ora pigliamo l’Universo Conosciuto (UC) che ha un diametro di 96 miliardi di anni-luce. Quante Laniakea ci stanno, in fila indiana? 185. Quindi da est a ovest o da nord a sud in UC ci puoi piazzare 185 superammassi, non uno di più. E anche 185 è un numero facilmente concettualizzabile. Infine, possiamo facilmente dire che nell’UC ci stanno – in lunghezza o in larghezza – 960.000 Via Lattea, una attaccata all’altra. E’ un botto, siamo d’accordo, ma dimostra subito che l’UC non è questa infinità che ci vogliono far immaginare. Se poi vogliamo credere alle stime più recenti, la VL è molto più grande di quanto si pensava anche solo 10-20 anni fa, e il milione scarso diventa un misero 384.000.
La cosa si fa un po’ meno immediata quando alla fine del discorso dobbiamo cubare, per vedere come stiamo in termini di volumi. 185 al cubo fa 6 milioni e 292 mila. Quindi in tutto l’universo conosciuto ci stanno 6 milioni e rotti di superammassi, che non sono pochi ma nemmeno troppi.
Purtroppo è quasi impossibile calcolare il numero di stelle, perché i superammassi sono strutture in gran parte vuote, con una densità di materia molto inferiore a quella delle galassie che li compongono.
I dati (puramente indicativi) sulla quantità di materia però ci sono: 10^17 masse solari per Laniakea, che poi puoi moltiplicare per i 6 milioni di cui sopra, che fa 10^23. Come piace ai giornalisti: 100.000.000.000.000.000.000.000 masse solari. Ci dice qualcosa? A me no: preferisco fermarmi alle lunghezze e ai volumi.
Alla fine della fiera, ora riesco a concettualizzare le dimensioni di UC? Sì, in soli due passaggi: dalla Via Lattea al superammasso e da qui all’universo. Ora ‘sti benedetti filamenti che ci propinano sui giornali so dove cominciano e dove finiscono. Alla faccia dei “divulgatori scientifici”.
Notarella finale
96 miliardi si può scrivere 9,6 x 10^10. Un anno-luce fa 9,46 x 10^15 metri. Moltiplicando, il diametro di UC è 9,1 x 10^26 metri.
All’altra scala di grandezza, quella del piccolo, sento ridere dalla tomba il buon Max Planck, la cui misura di lunghezza minima è – in metri – 1,6 x 10 elevato alla meno TRENTACINQUE: 1,6 x 10^-35. Perciò un essere umano, la cui scala di grandezza è un metro, è molto – ma proprio molto – più “grande” che “piccolo”. Per la precisione, un miliardo di volte.